In the first session we are going to learn about basic questions of philosophy of mathematic from Øystein Linnebo's book "Philosophy of Mathematics".
In the second session we get familiar with the roots of formal logic, formal proofs, and deductivism in mathematics.
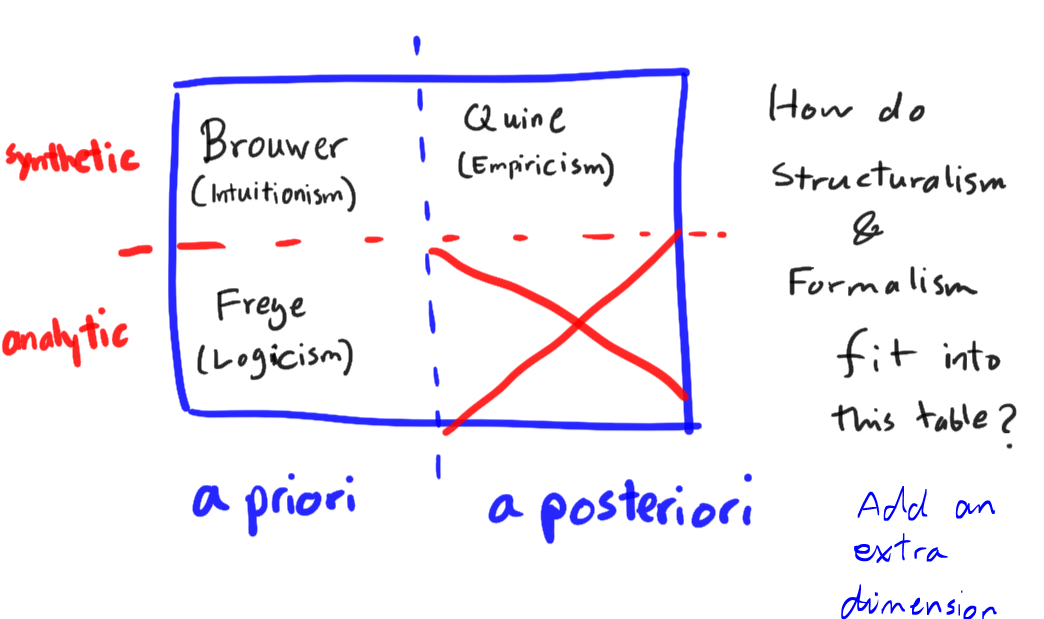
Note that Linnebo advocates a sort of Fregean Platonism.
Integration Challenge
The challenge is to integrate
- the metaphysics of mathematics (namely, what mathematics is about), with
- its epistemology (namely, how we form
our mathematical beliefs).
Integration challenge in basic terms
A Platonist should answer the following pressing question(s):
-
"How is it that our ways of forming mathematical beliefs are responsive to what mathematics is about?"
-
"How are the practices and mechanisms by which we arrive at our mathematical beliefs conducive to finding out about whatever reality mathematics describes?"
-
"Why is it not just a happy accident that our mathematical beliefs tend to be true?" There must be something about what we do that keeps us on the right track.
Linnebo insists that these questions have scientific answers:
"Just as science can be used to study navigation in birds and primates’ knowledge of their environment, it can also be used to investigate human knowledge of mathematics"
And
He holds that the mild circularity does not trivialize the question.
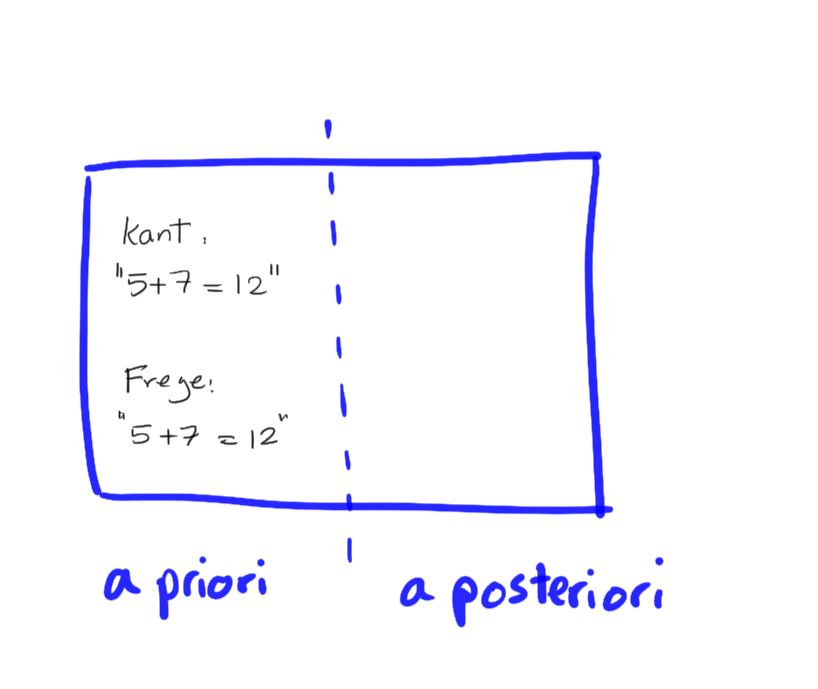
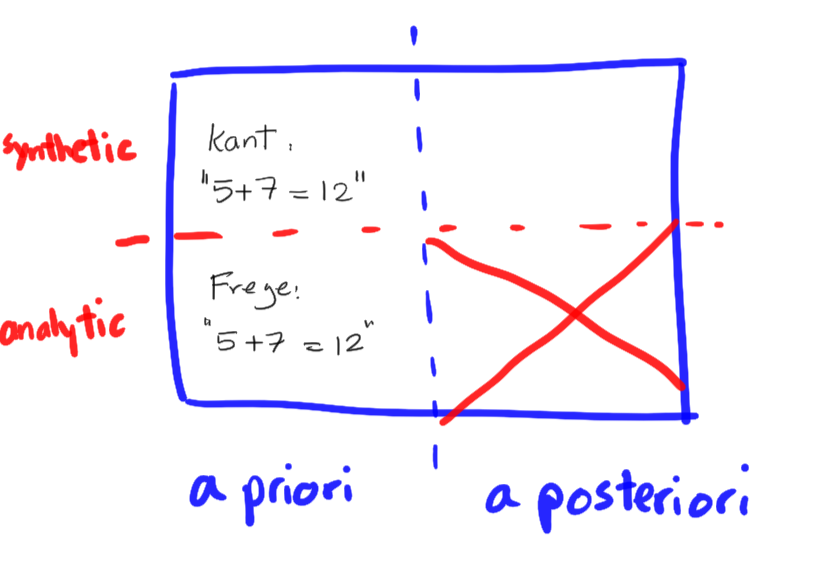
The first philosopher who helps us to have a shot at the "intergration challenge" is Immanuel Kant with his Analytic-Synthetic distinction.
Kant only deals with judgements which are made up of a subject and a predicate, e.g. "Bodies are extended."
They have simple subject-predicate form "A is B."
Kant defines a judgment as
analytic if
the predicate B belongs
to the subject A as something that is (covertly) contained in this
concept A.
The predicate expresses nothing which isn’t already contained in the subject.
e.g. "Bodies are extended."
By contrast the statement "bodies have weight" is synthetic.
The predicate amplifies (rather than explicates) the subject.
-
Kant agrees with the traditional view that all mathematical knowledge is a priori.
-
Naturally, the knowledge of a analytic statement is a priori.
-
The truly novel part of his view is that, despite being a priori, mathematical knowledge (including both arithmetic and geometry) is synthetic.
Examples:
-
The statement "7+ 5 = 12" is knowable a priori; it’s nevertheless synthetic. Kant's reason:
The concept of twelve is by no means already thought merely
by my thinking of that unification of seven and five.
-
Consider the statement "A straight line is the shortest path between two points."
The concept of the shortest is therefore altogether additional and cannot be obtained by any analysis of the concept of the straight line.
According to Kant, all synthetic a priori mathematical knowledge is necessary but not directly so; we need a "necessarily present intuition" which supplies the synthetic part of the judgement or statement.
To establish that the shortest line between two points is straight we need to bring in intuition to draw—perhaps in "pure imagination"— the shortest line between two points. We can then perceive that this line is straight.
Problems with the distinction above:
-
Since Kant's time, the language of mathematics has developed to include far more complex statements, e.g.
statements with bounded and unbounded quantifications, probabilistic statements, etc. Kant's analytic-synthetic distinction does not consider these statements.
-
The word "contain" in the definition of analyticity dependes on the underlying logic. Kant's logic is restricted to Aristotle's syllogism which is too restrictive for the purposes of doing any modern mathematics.
Compared to Kant, Frege conceives an extended logic and with it a fatter notion of analyticity. With this extended logic, Frege aimed to show that truths of arithmetic are analytic.