Linear Algebra (Math 1600A)
Published:
- Linear Algebra I, Spring 2014
- Lecturer: Gord Sinnamon
- Activities:
- Running exercise classes
- Marking mid-term and final exams papers
- Private tutorials
- Proctoring final exam
Published:
Published:
Published:
Published:
Published:
Published:
Published:
2nd year undergraduate module, School of Computer Science, University of Birmingham 🇬🇧, 2015
1st year undergraduate module, School of Computer Science, University of Birmingham 🇬🇧, 2016
2nd year undergraduate module, School of Computer Science, University of Birmingham 🇬🇧, 2017
1st year undergraduate module, School of Computer Science, University of Birmingham 🇬🇧, 2017
I helped with teaching of this course in three academic years. This course was fun!
2nd year undergraduate module, School of Computer Science, University of Birmingham 🇬🇧, 2018
Published:
I gave two guest lectures on metaprogramming and tactic writing in Lean 4. This github repository hosts the lecture notes and code.
Published:
a parallel development of Algebraic Weak factorization systems in Lean 3 and UniMath
Published:
Contributed to two projects of Condensed Mathematics formalization during the Copenhagen Master Class (joint with Jon Eugster and Dagur Tómas Ásgeirsson)
Published:
Weak factorization systems and Quillen model structures in Lean4
Published:
Wrestling with the dependent equalities
Published:
Polynomial Functors categorify polynomial functions. This repository provides a Lean 4 formalization of the theory of Polynomial Functors.
Published:
My talk at the Prospects of Formal Mathematics at the Hausdorff Institute in Bonn (02 Aug 2024):
Published:
Synthetic theories such as homotopy type theory axiomatize classical mathematical objects such as spaces up to homotopy. Although theorems in synthetic theories translate to theorems about the axiomatized structures on paper, this fact has not yet been exploited in proof assistants. This makes it challenging to formalize results in classical mathematics using synthetic methods. For example, Cubical Agda supports reasoning about cubical types, but Cubical proofs have not been translated to proofs about cubical set models, let alone their topological realizations.
Published:
Published:
Principles, tips and tricks
Published:
November 7-10, 2014
Published:
July 13-17, 2015
Published:
August 8-13, 2015
Published:
November 23-27, 2015
Published:
April 7-8, 2016
Published:
July 4-8, 2016
Published:
July 10-14, 2017
Published:
June 21-26 June, 2018
Published:
June 24-29, 2018
Published:
August 13-17, 2018
Published:
September 11-15, 2018
Published:
PSSL 98, 100, 101, 103, 104
Published:
July 2-5, 2019
Published:
18-20 December 2019
Published:
August 17 - 20, 2020
Published:
Meetings 6, 7, 13 – 23
Published:
13-17 October 2021
Published:
February 8, 2022 - March 7, 2022
Published:
28 June 28 - 1 July, 2022
Published:
July 11 - 15, 2022
Published:
January 9, 2023
Published:
January 16, 2023
Published:
February 13-17, 2023
Published:
May 21-26, 2023
Published:
June 26-30, 2023
Published:
July 2-8, 2023
Published:
July 8-12, 2023
Published:
April 16, 2024
Published:
June 23, 2024 - June 27, 2024
Published:
May – August 2024
Published:
2020
Published:
2020
Published:
2019 - 2021
Published:
2018 - present
Published:
Notes for my CARGO talk.
Published:
A list of tricks/theorems/constructions/concepts/theories I wished to know but never had time/opportunity to learn them!
Published:
Notes from a talk given by Nicola Gambino in theory seminar
Published:
Notes for my CARGO talk.
Published:
Some remarks and supplementary notes on my CARGO talk
Published:
Notes for my CARGO talks.
Published:
An example of a topos (from logic) that does not have any points.
Published:
Notes on Street’s paper
Published:
Some notes on my undertanding of derived algebraic geometry
Published:
Notes on framed bicategories based on a Cargo Talk
Published:
Some notes on generalization of Grothendieck fibrations to n-categories
Published:
Extended notes based on Steve Vickers’s expository talk in CARGO
Published:
Notes from my Lab Lunch talk on February 13, 2018
Published:
Notes on framed bicategories based on a Cargo Talk
Published:
Published:
Published:
Incomplete as they stand (May, 2017)
Research notes: Incomplete
Incomplete as they stand (May, 2017)
To be completed!
Incomplete as they stand (February, 2018)
To be wirtten soon!
Incomplete as they stand (April, 2018)
Warning: in construction! We introduce three Grothendieck topologies on the category of based schemes; the Zariski, the étale and the fpqc topology
Incomplete as they stand (April, 2018)
A review of theory of principal bundles and higher principal bundles
Incomplete as they stand (April, 2018)
A review of theory of principal bundles and higher principal bundles
Incomplete as they stand (April, 2018)
A review of existing philosophical theories on mathematical understanding
University of Birmingham (UK)
Download Paper
with Steve Vickers
Published in Theory and Application of Categories (TAC)
Download Paper Cite Paper arXiv:1808.08291
with Steve Awodey, Nicola Gambino
Published in Selecta Mathematica
Download Paper Cite Paper arXiv:2110.14576
with Emily Riehl
Published in Mathematical Structures in Computer Science
Download Paper Cite Paper arXiv:2210.00078
Presented in Types 2025
Download Paper Cite Paper Lean blueprint Code
Published:
Published:
Published:
The result here was earlier presented at the Yorkshire and Midlands Category Theory Seminars (YaMCATS) and Ghent–Leeds Virtual Logic Seminar and also at CATS seminars at ILLC, UvA, Amsterdam.
Published:
A talk based on the paper “Kripke-Joyal forcing for type theory and uniform fibrations” with Steve Awodey and Nicola Gambino.
Published:
An earlier version of this talk was given at JHU Category Theory SeminarSeminars.
Published:
In Fall 2022, I taught an undergraduate course in the Mathematics Department at Johns Hopkins University entitled “Introduction to Proofs” entirely with the Lean Proof Assistant. In this talk, I will report on this teaching experiment.
Published:
A modular approach to fibred in Lean 4
Published:
A game to learn linear algebra in Lean4 at Heinrich Heine University, Düsseldorf
Published:
Published:
Upper level undergraduate math course, Johns Hopkins University 🇺🇸
This course introduces students to the natural deduction style of encoding proofs in intuitionistic propositional logic and first order logic. Proof strategies such as proof by cases, negation introduction, proof by contradiction, induction, etc are justified by natural deduction. Later, students are familiarized with proofs on abstract mathematical structures such as finite and infinite sets, ordered sets, metric spaces, and topological spaces. They are introduced to methods of writing proofs which are rigorous, readable, and elegant. Mathematical communication, both written and spoken, is emphasized throughout the course. In this course, students also explore proof-relevant mathematics by interacting with a proof assistant.
Upper level undergraduate math course, Johns Hopkins University 🇺🇸
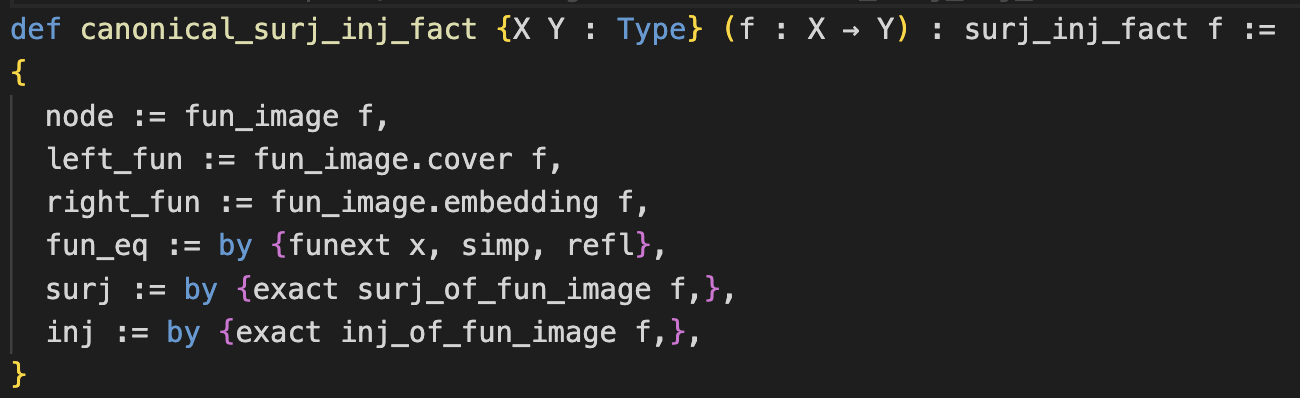
Upper level undergraduate course, Johns Hopkins University 🇺🇸
The emphasis is on fundamental mathematical ideas (basic functional analysis, reproducing kernel Hilbert spaces, concentration inequalities, uniform central limit theorems), basic statistical modeling techniques (e.g. linear regression, parametric and non-parametric methods), basic machine learning techniques for unsupervised (e.g. clustering, manifold learning), supervised (classification, regression), and semi-supervised learning, and corresponding computational aspects (linear algebra, basic linear and nonlinear optimization to attack the problems above). Applications will include statistical signal processing, imaging, inverse problems, graph processing, and problems at the intersection of statistics/machine learning and physical/dynamical systems (e.g. model reduction for stochastic dynamical systems).
Masters level course, Stockholm University 🇸🇪
Logic II is a second level logic course, giving an introduction to major topics of modern mathematical logic. It consists of three main parts: