Sina Hazratpour

Sina Hazratpour

Sitemap

A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.

Pages

Posts

Rilke

less than 1 minute read

Published:

For one human being to love another; that is perhaps the most difficult of all our tasks, the ultimate, the last test and proof, the work for which all other work is but preparation. I hold this to be the highest task for a bond between two people: that each protects the solitude of the other.

Die Sonne sinkt

1 minute read

Published:

Friedrich Nietzsche, aus Dionysus-Dithyramben (1888)

On Mathematical Understanding

9 minute read

Published:

Warning: As it stands this write up is incomplete and half-baked! Read at your own risk!

Learning Dutch

less than 1 minute read

Published:

My way of learning dutch

How to think about liberty?

4 minute read

Published:

Isiah Berlin in his famous essay Two Concepts Of Liberty contrasted two notions of liberty: positive and negative. What are they and are there other forms of liberty in the 21st century social and political subjects outside of this dichotomy?

Tufte CSS

14 minute read

Published:

An elegant style

GTA

Linear Algebra (Math 1600A)

Published:

  • Linear Algebra I, Spring 2014
    • Lecturer: Gord Sinnamon
    • Activities:
      • Running exercise classes
      • Marking mid-term and final exams papers
      • Private tutorials
      • Proctoring final exam

Calculus 1225

Published:

  • Methods of Calculus, Autumn 2014
    • Instructors: Stuart Rankin, Gord Sinnamon, Vicky Olds
    • Activities:
      • Helping students on an individual basis in Help Center
      • Marking mid-term and final exams papers
      • Proctoring for final exams

Finite Maths (MATH 1228)

Published:

  • Methods of Finite Mathematics, Autumn 2013
    • Lecturer: Vicky Olds
    • Activities:
      • Running exercise classes
      • Marking mid-term and final exams papers
      • Private tutorials

comp-training

Putnam Training Sessions

Published:

  • Putnam Training Sessions, Autumn 2013 & Autumn 2014
    • The William Lowell Putnam is a mathematics contest for undergraduates in Canada and the U.S. This year’s contest will be written on Saturday, December 6th. Additional information can be found at math.scu.edu/putnam/
    • Preparation sessions for the Putnam Mathematics Competition are run by the Math department and are open to all students interested in mathematical problem-solving. There will be an organizational meeting for the Preparation sessions this Friday, September 26th at 5pm in MC 108 (in Middlesex).
    • Exercise material: Putnam and Beyond by Gelca and Andreescu

demonstration

Mathematics for Computer Science (Spring 2016)

1st year undergraduate module, School of Computer Science, University of Birmingham, 2016

  • Introduction to Mathematics for Computer Science, Semester 2, 2016
    • Module Lecturer: Steve Vickers
    • Content:

      • Coordinate geometry: Equations of lines and circles; gradients.
      • Functions and their graphs: A very vivid way to describe functions and their properties.
      • Functions at large x: This aspect of functions is interesting in its own right, but also important for analysing the efficiency of computer algorithms.
      • Differential calculus: Rules for finding gradients. This lies right at the heart of mathematical applications.
      • Differential calculus continued.
      • Polynomials: Manipulating them, and something about finding their roots.
      • Trigonometry: Calculating with angles.
      • Complex numbers: What happens if you invent an "imaginary" square root of -1. The amazing idea that trigonometry is just imaginary exponentiation.
      • Integration: Finding areas - or the opposite of differentiation.
      • Simultaneous linear equations: Solving linear equations simultaneously.

    • Activities:
      • Joinlty running exercise classes

Team Project Module (Spring 2017)

2nd year undergraduate module, School of Computer Science, University of Birmingham, 2017

  • Team Project, Semester 2, 2017
    • Module Lecturer: Ian Kenny
    • This year’s theme: Video Game Design in Java
    • Core features of the game:

      • Competitive play.Your game must allow players to compete.
      • Networking.Your game must allow multiple players to play across a network. The specific net-working arrangement depends on the type of game but, for example, you might create a client-server typearrangement in which multiple clients connect to a controlling server, or a server performing some otherservice.
      • Artificial Intelligence.Your game must have the option of computer-controlled players. These mightbe individual or team players, depending on the type of game.
      • User Interface.Your game must have a user interface, i.e. a convenient way for players to interactwith the game. This will almost certainly require a menu as a minimum but will more than likely alsorequire other interface entities such as dialog windows that have a range of controls, clickable icons, etc.The user interface will also include crucial feedback information for the player.

  • Activities:
    • Supervising projects
    • Helping students in the Lab on an individual basis
    • Meeting students in office hours

Models Of Computation (Spring 2017)

2nd year undergraduate module, School of Computer Science, University of Birmingham, 2018

lean-projects

Condensed Mathematics in Lean 4 Permalink

Published:

Contributed to two projects of Condensed Mathematics formalization during the Copenhagen Master Class (joint with Jon Eugster and Dagur Tómas Ásgeirsson)

meetings

QPL 2015

less than 1 minute read

Published:

July 13-17, 2015

IHES Topos

less than 1 minute read

Published:

November 23-27, 2015

Toposes In Como

less than 1 minute read

Published:

June 24-29, 2018

WoLLIC 2019

less than 1 minute read

Published:

July 2-5, 2019

HoTT MURI

less than 1 minute read

Published:

28 June 28 - 1 July, 2022

meetings-online

notes

A learning wishlist

Published:</strong>

A list of tricks/theorems/constructions/concepts/theories I wished to know but never had time/opportunity to learn them!

A topos without points

Published:</strong>

An example of a topos (from logic) that does not have any points.

places

portfolio

Three Sites Of Relative Schemes

Incomplete as they stand (April, 2018)

Warning: in construction! We introduce three Grothendieck topologies on the category of based schemes; the Zariski, the étale and the fpqc topology

Principal Bundles

Incomplete as they stand (April, 2018)

A review of theory of principal bundles and higher principal bundles

Principal Bundles

Incomplete as they stand (April, 2018)

A review of theory of principal bundles and higher principal bundles

publications

PhD Thesis

Published in University of Birmingham (UK), 2019

Under supervision of Steve Vickers

talks

Kripke Joyal Semantics For Dependent Type Theory

Published:

The result here was earlier presented at the Yorkshire and Midlands Category Theory Seminars (YaMCATS) and Ghent–Leeds Virtual Logic Seminar and also at CATS seminars at ILLC, UvA, Amsterdam.

Teaching Introduction To Proofs With Lean

Published:

In Fall 2022, I taught an undergraduate course in the Mathematics Department at Johns Hopkins University entitled “Introduction to Proofs” entirely with the Lean Proof Assistant. In this talk, I will report on this teaching experiment.

teaching

Introduction to Proofs (Fall 2021 & Spring 2022)

Upper level undergraduate math course, Krieger 304, Homewood Campus, Johns Hopkins University

This course introduces students to the natural deduction style of encoding proofs in intuitionistic propositional logic and first order logic. Proof strategies such as proof by cases, negation introduction, proof by contradiction, induction, etc are justified by natural deduction. Later, students are familiarized with proofs on abstract mathematical structures such as finite and infinite sets, ordered sets, metric spaces, and topological spaces. They are introduced to methods of writing proofs which are rigorous, readable, and elegant. Mathematical communication, both written and spoken, is emphasized throughout the course. In this course, students also explore proof-relevant mathematics by interacting with a proof assistant.

Mathematical and Computational Foundations of Data Science (Spring 2023)

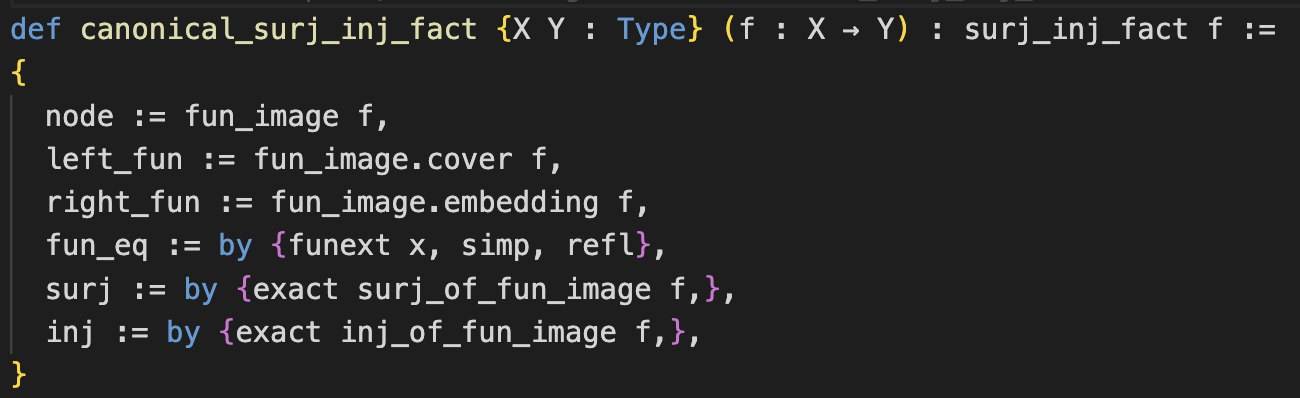
Upper level undergraduate course, Shaffer 300, Homewood Campus, Johns Hopkins University

Course Description

The emphasis is on fundamental mathematical ideas (basic functional analysis, reproducing kernel Hilbert spaces, concentration inequalities, uniform central limit theorems), basic statistical modeling techniques (e.g. linear regression, parametric and non-parametric methods), basic machine learning techniques for unsupervised (e.g. clustering, manifold learning), supervised (classification, regression), and semi-supervised learning, and corresponding computational aspects (linear algebra, basic linear and nonlinear optimization to attack the problems above). Applications will include statistical signal processing, imaging, inverse problems, graph processing, and problems at the intersection of statistics/machine learning and physical/dynamical systems (e.g. model reduction for stochastic dynamical systems).